Levenshtein Distance

Definition

The Levenshtein distance between two strings a , b (of length

a

and

b

respectively) is given by lev(a,b) where

where the tail of some string x is a string of all but the first character of x, and x[n] is the nth character of the string x, counting from 0.

Note that the first element in the minimum corresponds to deletion (from a to b), the second to insertion and the third to replacement.

This definition corresponds directly to the naive recursive implementation.

Steps

Initialization

First we need to create a 2D array of size n and m where n is the number of characters in word1 + 1 and m is the number of characters in word2 + 1.

Then, we will loop through the first column and row of the array and initialize them to there index with respect to n for row and m for column.

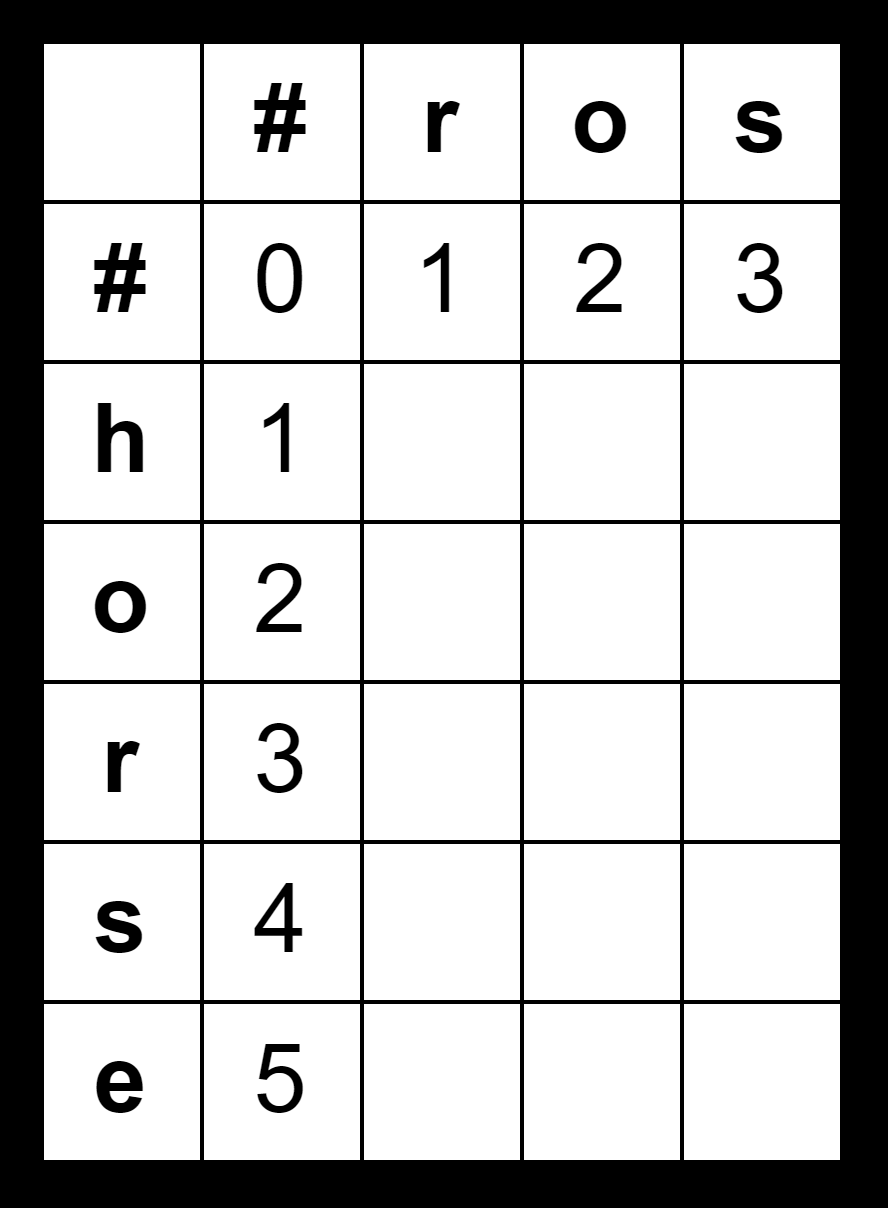
Find the Distance

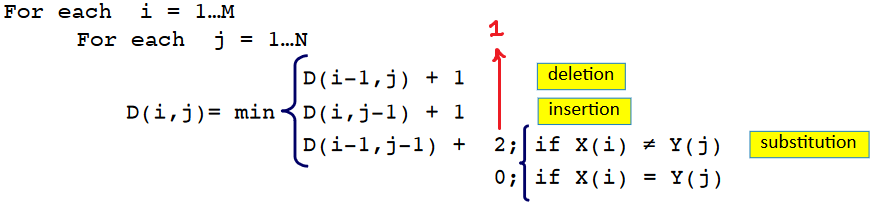
The above figure is the for loop that will be used to find the distance. In this case though we have to replace the 2 with 1 so that we can keep track of how many edits we did.

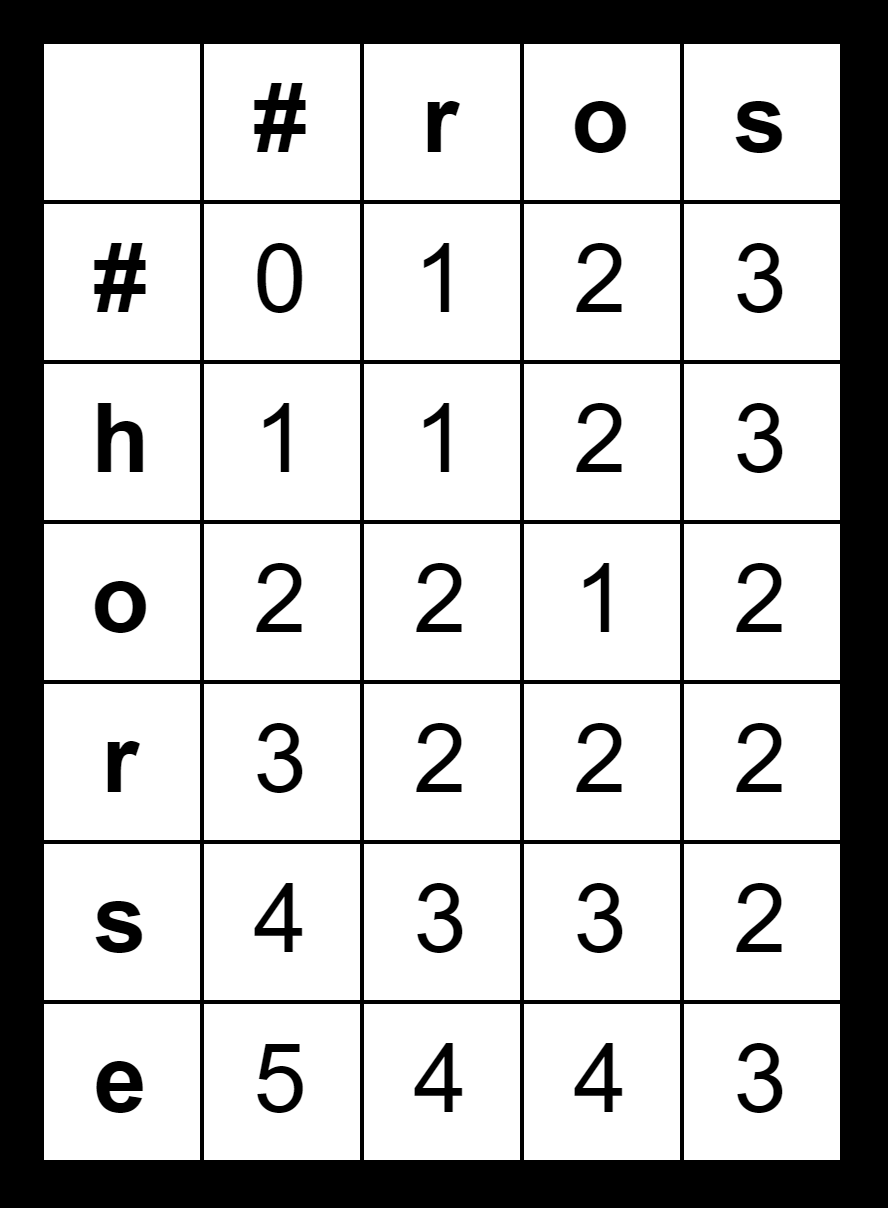
Result

• D(m,n) is the distance, in this example it’s 3

Code

• Java

class Solution {
    public int minDistance(String word1, String word2) {
        int row = word1.length();
        int col = word2.length();
        int[][] ed = new int[row + 1][col + 1];
        for(int i = 0; i <= row; i++)
            ed[i][0] = i;
        for(int j = 0; j <= col; j++)
            ed[0][j] = j;
        for(int i = 1; i <= row; i++) {
            for(int j = 1; j <= col; j++) {
                if(word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    ed[i][j] = ed[i - 1][j - 1];
                } else {
                    int dia = ed[i - 1][j - 1];
                    int hor = ed[i][j - 1];
                    int ver = ed[i - 1][j];
                    if(dia <= hor && dia <= ver)
                        ed[i][j] = dia;
                    else
                        ed[i][j] = ver < hor ? ver : hor;
                    ed[i][j]++;
                }
            }
        }
        return ed[row][col];
    }
}

Complexity

• Time: O(n * m)
• Space: O(n * m)